22.02.09 - Matrices

Numeric Vector Matrices Matrix Operations: Sum and Product Determinant of a Matrix

Numeric Vector

Numeric Vector

• Let $n\in \N$ and $n>0$
• Indicated with $\R^n$, set of ordered n-tuples of real numbers
• Generic element a = ($a_1,a_2,...,a_n$) is named numeric vector or simply vector of order n

Sum of Vectors

• Sum of vectors: $c = (a_1 + b_1 , a_2 + b_2 , . . . , a_n + b_n )$
• Can also do the same for $a-b$

Scalars

Numeric value $\lambda \in \R^1$ is a scalar The product of a vector by a scalar is the vector $c=(\lambda a_1,\lambda a_2,...,\lambda a_n)$ Very similar to $\times$

Scalar Product

Generated by the sum of the products of each pair of corresponding components $ab = c = a_1b_1 + a_2b_2,...,a_nb_n$ Example:

• $a = (1, 0, 3)$
• $b = (2, 1, −2)$
• $ab = (1 · 2) + (0 · 1) + (3 · (−2)) = 2 + 0 − 6 = −4$

Properties

• Symmetry: $ab=ba$
• Associativity: $\lambda (ba) = (\lambda a)b = a(\lambda b)$
• Distributivity: $a(b+c)=ab+ac$

Matrices

Matrix

2 natural numbers > 0. A matrix ($m\times n$) is a generic table of the kind

$A=\begin{pmatrix} a_1,_1&a_1,_2&...&a_1,_n \\ a_2,_1&a_2,_2&...&a_2,_n \\ ...&...&...&...\\ a_m,_1&a_m,_2&...&a_m,_n \\ \end{pmatrix}$ where each matrix element $a_i,_j\in \R$

• m=rows, n=columns
• n order square matrix - $A \in \R_n,_n$
• rectangular - $m \ne n$

Matrix Transpose

• Transpose matrix is $A^T$ whose elements are the same of A but $\forall i,j : a_j,_i = a^T_i,_j$
• Change index of row with index of columns (rotate it)

Symmetry

• Only on square matrix
• When $\forall _i,_j : a_i,_j = a_j,_i$

Diagonal and Trace

• Diagonal of a matrix is the ordered n-tuple that displays the same index twice. From 1 to $n a_i,_j$
• Trace is the sum of the diagonal elements tr($A$)

Null Matrices

• Is said null $O$ if all elements are zeros

Identity Matrices

• Square matrix whose diagonal elements are all ones while all the other extra-diagonal elements are zero

Matrix Operations: Sum and Product

Matrix Sum

$\forall i,j:c_i,_j = a_i,_j + b_i,_j$ Both matrices must be the same size! Can be subtracted from one another

Properties of the matrix sum

• commutativity: $A + B = B + A$
• associativity: $(A + B) + C = A + (B + C)$
• neutral element: $A + O = A$
• opposite element: $∀A ∈ Rm,n : ∃!B ∈ R m,n \ni ‘ A + B = O$

Product of a scalar and a matrix

Matrix $C$ defined as: $\forall i,j:c_i,_j = \lambda a_i,_j$ Similar to $\times$ by the scalar

Properties of multiplying by a scalar

• associativity: $\forall A \in \R_m,_n$ and $\forall \lambda , \mu \in \R$:
  • $(\lambda \mu )A = (A\mu ) \lambda = (A \lambda) \mu$

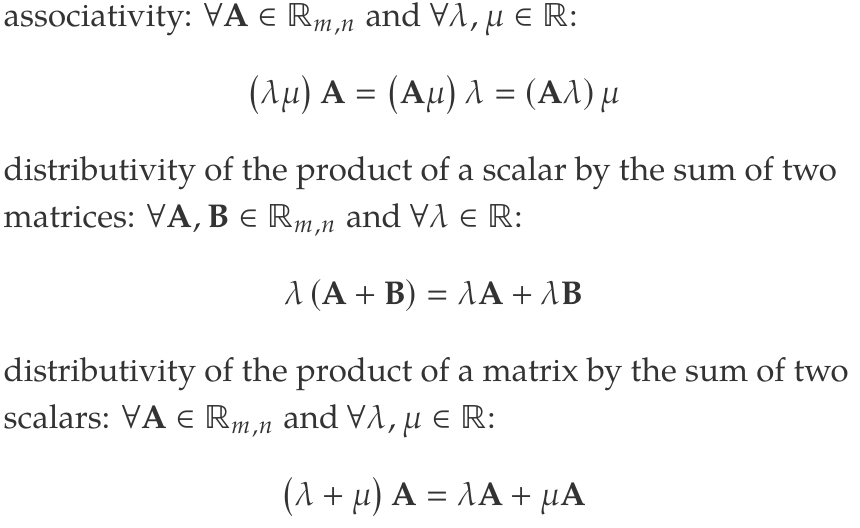
Matrix product

Product of matrices $A$ and $B$ is a matrix $C = AB$

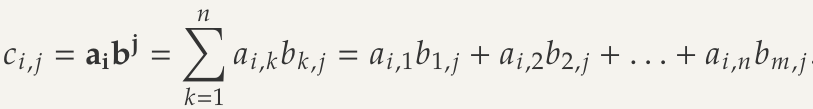
• Just the scalar product of row vectors of $A$ with column vectors of $B$
• Number of columns in the first matrix must be the same as the number of rows in the second

$c_2,_1 = a_2b^1$

• left distributivity: $A (B + C) = AB + AC$
• right distributivity: $(B + C) A = BA + CA$
• associativity: $A (BC) = (AB) C$
• transpose of the product: $(AB)^T = B^T A^T$
• neutral element: $\forall A : AI = A$
• absorbing element: $\forall A : AO = O$

Commutable - $AB=BA$, one with respect to the other Every matrix $A$ is commutable with $O$ (and the result is always $O$) and with $I$ (and the result is always $A$)

Determinant of a Matrix

(takes decades to understand)

• Most important concepts of maths

• Permutation: Different ways of grouping items, can be checked with factorials
• Fundamental Permutation - Reference a sequence
• Inversion - Every time two objects in a permutation follow each other in a reverse order with respect to the fundamental
• Even class permutation - Permutation undergone to an even number of inversions
  • Also have Odd class permutation

Associated Product

Never in the same column/row. Product of this is referred to as associated product and is indicated with the symbol $\epsilon$(c). Wont be the same number either. Order the factors according to the row index:

Coefficient of nk

Consider 1-2-...-n as fundamental permutation, the scalar nk is defined as:

Determinant of a Matrix

indicated as det $A$ is the function det: $\R_n,_n \to \R$ defined as the sum of n! associated products: $\sum ^{n!} _{k=1} ....$ Do it as left to right diagonal +, then right to left diagonal as -

Linear Dependence/Independence

Linear Combination

If row can be represented by other rows with weighted sum by means of the same scalars

Linear dependence

If null vector can be expressed as the linear combination of the $m$ rows ($n$ columns) by means of nun-null scalars Rows are linearly dependent if

$\exists \lambda_1,\lambda_2,...,\lambda_m\ne0,0,...,0$ such that

Linear Independence

If only way to express a row of all zeros as the linear combination of the m rows(n columns) is by means of null scalars

Fundamental property of Linear Dependence

r rows are linearly dependent if and only if at least one row can be expressed as the linear combination of the others